
In $z$ direction the solutions within each layer are analytically matched. In $x$ direction the filed is expanded into Bloch waves within each layer. show ()ĭivision of a periodic grating into layers for RCWA. set_title ( 'Sparse system matrix A', y = 1.08 ) ax2.

plot_trisurf ( points, points, c, triangles = tri. add_subplot ( 1, 2, 2, projection = '3d' ) cntr = ax1. zeros ( len ( points )) # at inner points c = A^-1 v c = solve ( A, v ) # = Plot results = fig = plt. dot ( grad_psi ( * c, k2 )) # Solution vector c such that u(x,y) = sum_i c_i psi_i(x,y) c = np. Hence, we can # multiply the integrand value in the center of the simplex # times the area of the simplex A += a * grad_psi ( * c, k1 ). ones ( 3 )))) for k1 in simplex : if not is_inner : continue # the integral of the basis function over the simplex is equal # to the volume of a three sided pyramid of height 1 v += a / 3 for k2 in simplex : if not is_inner : continue # The gradient is constant over the simplex.
sum ( coords, axis = 0 ) / 3 #area of simplex a = 0.5 * np. array ( for p in simplex ]) #center of simplex c = np. zeros ( len ( mask_inner )) for simplex in tri. zeros (( len ( mask_inner ), len ( mask_inner ))) # Right-hand side for f(x,y) = 1 v = np. # At inner node k it holds psi_k(p_k) = 1 and otherwise psi_k(p_k') = 0 psi = # Gradients of basis functions def grad_psi ( x, y, k ): return approx_fprime (, psi, epsilon = 1e-6 ) # System matrix defined for basis functions belonging to inner nodes # Note that all these basis functions go to zero at the boundary. show ()įrom scipy.interpolate import LinearNDInterpolator from scipy.optimize import approx_fprime from scipy.linalg import solve from mpl_toolkits.mplot3d import Axes3D # The basis consists of piecewise linear functions. title ( 'Triangulation of computational domain' ) plt. where ( is_inner ) # Plot triangulation fig = plt.

arange ( len ( points )) < len ( points ) - n mask_inner = np. column_stack (( x, y )))) # Make Delauney triangulation of mesh points tri = Delaunay ( points ) # Last n points are at boundary, others are inner points is_inner = np. arange ( n ) / n r_shape = r * r_boundary ( angles ) x, y = r_shape * np. pi * r / slc ) #number of points on radius angles = 2 * np. array (]) # start with central point for r in radii : n = np. linspace ( slc, 1, int ( 1 / slc )) points = np. sin ( 3 * angle ) slc = 0.15 #side length constraint for triangulation radii = np.

#Angle-dependent radius of boundary Omega def r_boundary ( angle ): return 1 + 0.12 * np. Import numpy as np from scipy.spatial import Delaunay import matplotlib.pyplot as plt % matplotlib inline That is, $A$ is a sparse matrix and it therefore typically inverted with a specialized sparse matrix solver.
FEM VS FDTD FULL
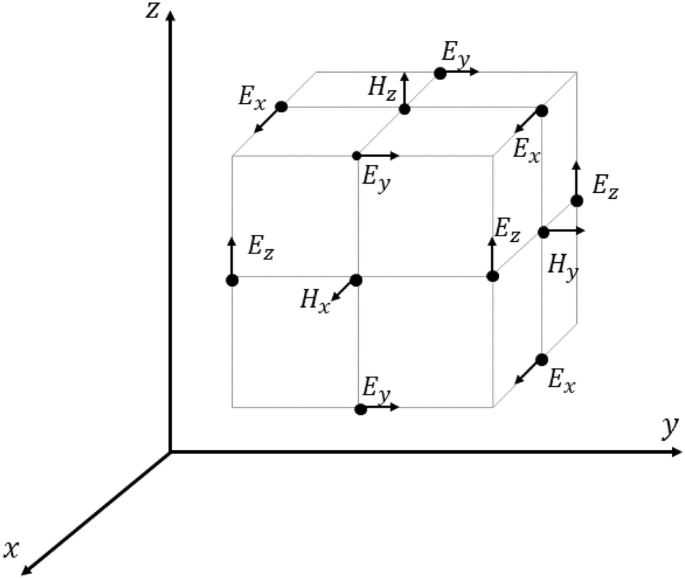
In order to resolve wave optics phenomena like diffraction, optical resonances, and interference, the full Maxwell equations in matter have to be solved, that describe the behavior of the full electric field $\mathbf = ^T$ evaluates toīecause each element is connected to only a few neighboring elements, most of the entries of the system matrix are zero. The behavior of nano-optical systems can in general not be described by ray optics.


 0 kommentar(er)
0 kommentar(er)
